بهترین معماری‌های شبکه عصبی گراف(GNN): GCN، GAT، MPNN و موارد دیگر

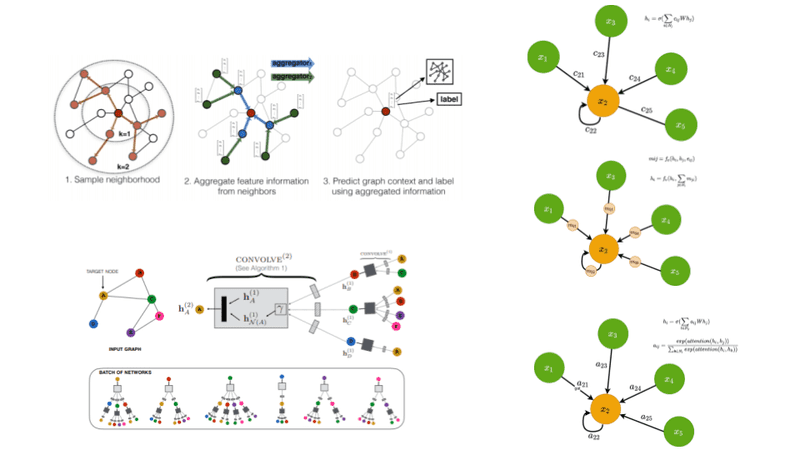
از گذشته، مجموعه داده‌های بکار رفته در برنامه‌های یادگیری عمیق همانند بینایی کامپیوتر و پردازش زبان طبیعی (Natural Language Processing) یا به اختصار، NLP معمولا در فضای اقلیدسی ارائه می شود. با این وجود، تعداد داده‌های غیر اقلیدسی که بصورت گراف (Graph) نشان داده می شود، در حال افزایش است.

در این راستا، از شبکه‌های عصبی گراف (GNNs) به منظور اعمال روش‌های یادگیری عمیق در گراف‌ها استفاده می شود. قابل ذکر است که اصطلاح GNN بطور معمول به انواع الگوریتم‌های متنوع اطلاق می گردد و به یک معماری واحد اشاره ندارد. همانطور که در ادامه ارائه خواهد شد، مجموعه‌ای از معماری‌های مختلف در طول سال‌ها توسعه یافته اند. برای نمونه ، در شکل زیر مهمترین مقالات منتشر شده در این زمینه آورده شده است. این دیاگرام برگرفته از مقاله مروری ( به انگلیسی Review article ) با موضوع GNN توسط J.Zhou و همکاران است.

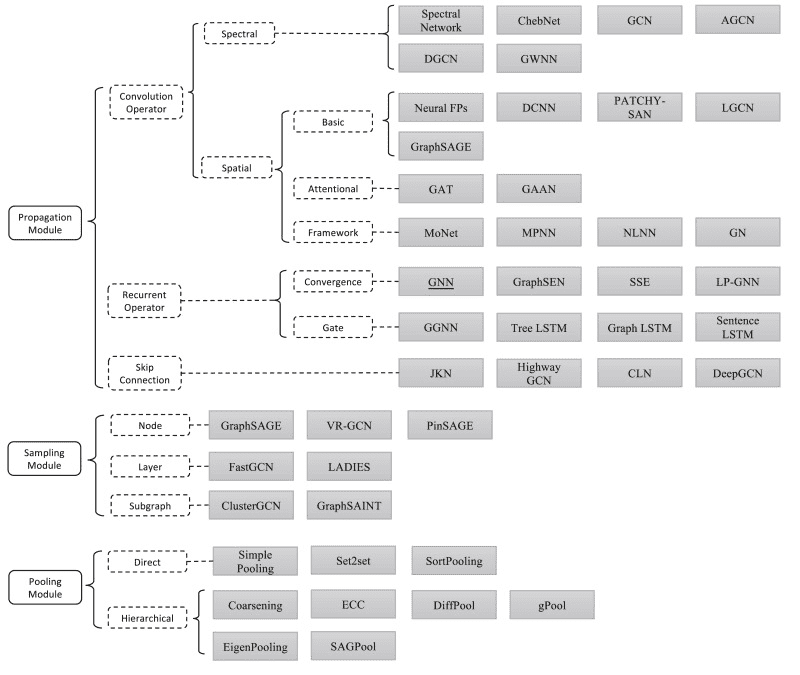
منبع: Graph Neural Networks: A Review of Methods and Applications ¹

قبل از پرداختن به انواع معماری‌ها، بهتر است، چند تعاریف پایه و برخی نشانه‌گذاری را شرح دهیم.

تعاریف پایه و نشانه‌گذاری در گراف‌ها

گراف ها از مجموعه رئوس (گره‌ها) و یال‌ها (پیوند‌های اتصالی بین گره‌ها) تشکیل شده است که هر دو آنها می توانند مجموعه ای از ویژگی ها را داشته باشند. از این پس، بردار ویژگی گره‌ hi تعریف می شود که i معیار گره است. به طور مشابه، بردار ویژگی یال‌ها یا پیوند اتصالی بین گره‌ها با مشخصه eij تعریف می شود که i, j نماینگر گره‌های مورد اتصال است.

همانطور که می دانید، گراف‌ها می توانند جهت‌دار، غیر‌جهت دار و وزن‌دار ، غیر وزن‌دار باشند. بنابراین هر معماری ممکن است، فقط برای یک نوع گراف یا برای هر نوعی بکار گرفته شود.

حال می توانیم شروع به توسعه یک گراف شبکه عصبی کنیم ؟

منشاء اصلی ایده بیشتر معماری‌های GNN پیچیدگی گراف می باشد. در اصل، ما تلاش می کنیم ایده مربوط به پیچیدگی (کانولوشن) را به گراف‌ها تعمیم دهیم. گراف‌ها را می توان به عنوان تعمیمی از تصاویر مشاهده کرد که در آن هر گره مربوط به یک پیکسل متصل به 8 (یا4) همسایه مجاور است. از آنجاکه شبکه‌های عصبی پیچیده (CNNs) موفقیت برجسته خود مرهون ایده پیچیدگی (کانولوشن) است، چرا ما این ایده را به گراف‌ها تعمیم ندهیم؟

گراف پیچشی (کانولوشنی)

گراف پیچشی (کانولوشن) ویژگی‌های گره در لایه بعدی را به عنوان تابعی از ویژگی‌های مجاور پیش بینی می کند. به عبارت دیگر، ویژگی‌های گره xi در یک فضای نهفته hi که می توان به دلایل مختلف مورد استفاده قرار گیرد، انتقال می یابد.

$x\:_{i}\:−>h\:_{i}$

به صورت تصویری می توان به صورت زیر نمایش داد :

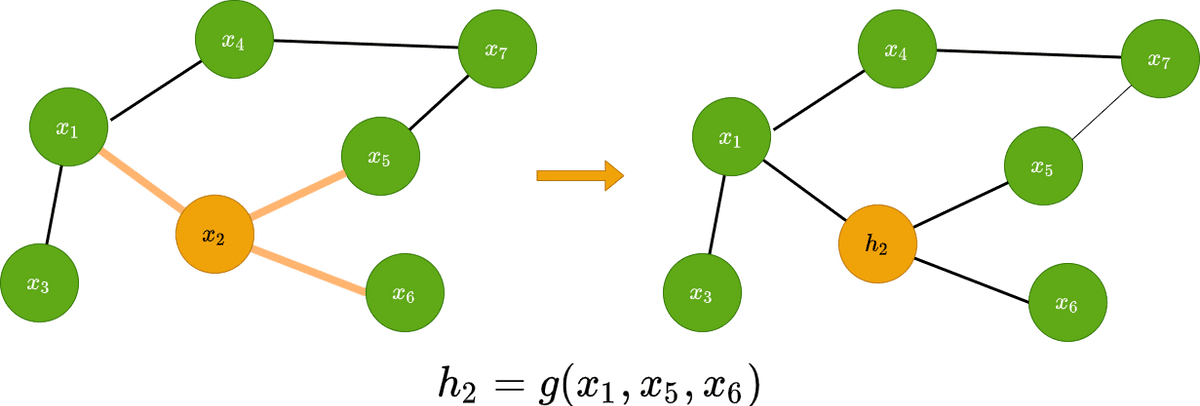
با این وجود، با این ویژگی بردار گره نهفته در واقع ما چه می توانیم انجام دهیم؟ به طور کلی همه برنامه‌های موجود در یکی از دسته بندی های زیر جای می گیرد:

طبقه بندی گره
طبقه بندی یال (پیوند بین گره)
طبقه بندی گراف

طبقه بندی گره

اگر یک تابع مشترک f را به هر یک از بردارهای نهفته h_i اعمال کنیم. در اینصورت می توانیم هر یک از گره‌ها را پیش بینی کنیم. به این ترتیب می توانیم گره‌ها را بر اساس ویژگی‌های شان طبقه بندی کنیم:

$Z\:_{i}\:=f\left(h\:_{i}\:\right)$

طبقه بندی یال (پیوند بین گره)

به طور مشابه، می توانیم از آن برای طبقه‌بندی یال‌ها بر اساس ویژگی‌های شان استفاده کنیم. به این منظور، درصورت وجود به دو بردارهای گره مجاور همچنین به ویژگی‌های یال لازم داریم. از نظر ریاضی داریم :

$Z\:_{ij}\:=f\left(h\:_{i}\:,h\:_{j}\:,e\:_{ij}\:\right)$

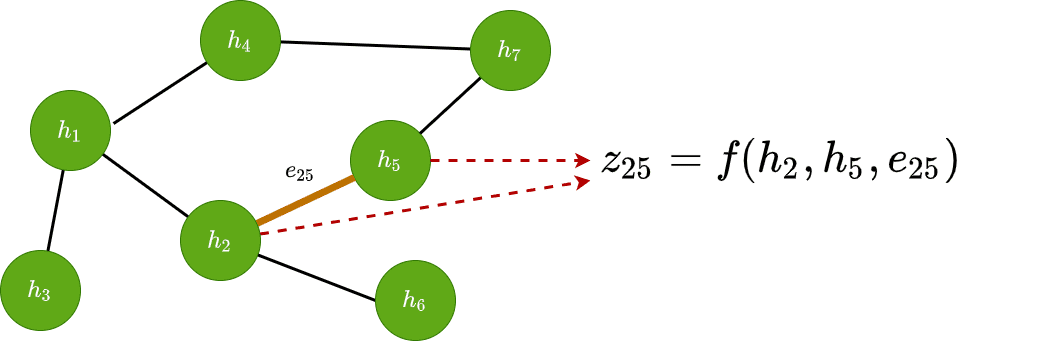
طبقه بندی گراف

در آخر، توسط تجمیع همه ویژگی‌های گره و اعمال یک تابع مناسب f ، می توانیم برخی مشخصه‌ها را برای کل گراف پیش بینی کنیم.

$Z\:_{G}\:=f\left(\:\sum_{i}^{} \:h\:_{i}\:\right)$

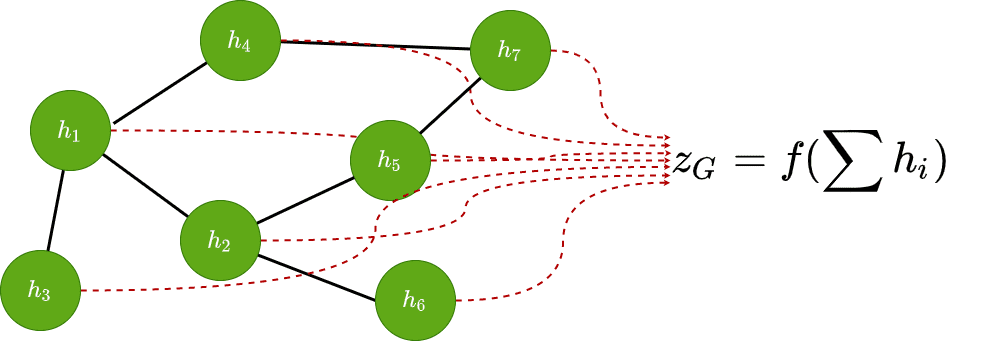
معمولا نتیجه تجمیع یک تابع تغییرناپذیری جایگشت¹ همانند مجموع، عملیات میانگین، عملیات ادغام یا حتی یک لایه خطی قابل آموزش می باشد.

یادگیری استقرایی در مقابل فراگیری انتقالی

اصطلاح “استقرایی در مقابل انتقالی” که معمولا در زمینه GNN استفاده می شود، می تواند کمی گنگ به نظر برسد. بنابراین در ادامه به تعاریف آن می پردازیم.

در یادگیری انتقالی، قبلا مدل توسط داده‌های ورودی آزمون و آموزش مواجه می شود. در مسئله ما اینها گره‌های از یک گراف بزرگ هستند که قصد انجام پیش بینی مشخه‌های گره‌ را داریم. درصورت افزودن یک گره به گراف، لازم است مدل مجدد آموزش داده شود.

در یادگیری استقرایی، مدل فقط متوجه داده‌های آموزشی است. بنابراین می توانیم از مدل ایجاد شده به منظور پیش بینی مشخصه‌های گراف برای داده‌های پنهان استفاده کنیم.

برای فهم بیشتر این موضوع را از دیدگاه GNN‌ها با یک مثال زیر متصور می شویم. یک گراف با 10 گره را در نظر بگیرید. در ضمن ساختار گراف و نحوه اتصال گره‌ها برای مثال زیر اهمیت ندارد. از آنها، 6 عدد برای مجموعه آموزشی (با مشخه‌ها یا برچسب) و به تعداد 4 عدد برای مجموعه آزمون(تست) استفاده می کنیم. حال سوال اینجاست، چگونه این مدل را آموزش می دهیم؟

از یک رویکرد یادگیری نیمه نظارتی²استفاده کنید و کل گراف را تنها با استفاده از 6 نقطه داده برچسب‌گذاری شده آموزش دهید که یادگیری استقرایی تلقی می گردد. مدل‎های آموزش دیده صحیح توسط یادگیری استقرایی، می توانند به خوبی تعمیم یابند اما تاحدودی به دست آوردن ساختار کل داده‌ها امری دشوار است.
از یک رویکرد خود نظارتی³ استفاده کنید که نقاط داده فاقد برچسب را با استفاده از اطلاعات اضافی، برچسب گذاری می کند و مدل را در هر 10 گره موجود آموزش می دهد. این نوع از یادگیری که در حوزه GNN بسیار رایج بوده، یادگیری انتقالی گویند، چرا که از کل گراف به منظور آموزش مدل استفاده می شود.

با وجود این مباحث، مطالب را با محبوب ترین معماری های GNN ادامه می دهیم.

متد‌های طیفی

متدهای طیفی با نمایش یک گراف در حوزه طیفی سر و کار دارند. ایده شهودی می باشد.

این روش‌ها بر پایه پردازش سیگنال گراف است و تعریفی از عملگر پیچش (کانولوشن) در حوزه طیفی را از طریق تبدیل فوریه F ارائه می دهد. سیگنال x گراف نخست به واسطه تبدیل فوریه F گراف به حوزه طیفی تبدیل می شود. سپس عملیات کانولوشن با استفاده از ضرب درایه ای (element-wise) انجام می دهیم. در نهایت، سیگنال حاصل به واسطه تبدیل فوریه معکوس F−1 گراف به دست می آید.

$F(x)=U^{T}x$

$F\:^\frac{-1}{}\:\left(x\right)=Ux$

که در اینجا U ماتریسی که توسط بردارهای ویژه L تعریف شده است. که در رابطه L=UΛUT ، Λ یک ماتریس قطری با مقادیر ویژه گراف می باشد. ( Λ=diag([λ0,…,λ1]))

عملگر کانولوشن را بصورت زیر تعریف می شود:

$g∗x=F^\frac{-1}{}\:\left(F\left(g\right)⋅F\left(x\right)\right)=U\left(U\:^{T}\:g⋅U\:^{T}\:x\right)$

L گراف نرمالیزه لاپسی می باشد که می توانیم بصورت زیر تعریف کنیم:

$L=I\rightharpoonup D^{\frac{-1}{2}}\:\:AD^{\frac{-1}{2}}$

U^Tg یک فیلتر در حوزه طیفی ، D ماتریس درجه و A ماتریس مجاورت گراف می باشد. برای تشریح بیشتر، مقاله در مورد کانلوشن‌های گراف را ملاحظه کنید.

شبکه‌های طیفی

شبکه‌های طیفی ² فیلتر را در حوزه طیفی به یک ماتریس قطری g_w کاهش دادند که در آنها w پارامتر‌های قابل یادگیر شبکه می باشند. در نتیجه، می توان یک شبکه ی به منظور یادگیری فیلتر‌های کانولوشنی برای طبقه‌بندی گراف درست کرد.

فیلتر بروی کل گراف اعمال می شود، بنابراین مفهوم منطقه‌ای یا محلی که در تصاویر است، وجود ندارد
از نظر محاسباتی ناکارآمد است، به ویژه در گراف های بزرگ

ChebNets

برای رفع مشکل محلی، ChebNets ³ یک پیشنهادی مبنی بر اینکه ارائه ویژگی هر برداری باید متاثر از k-hop مجاور خود باشد. با استفاده از بسط چبیشف (Chebyshev) از مرتبه K، می توانیم یک ضریب مکانی K (K-localized) کانولوشن تعریف کنیم که می تواند برای تشکیل یک شبکه عصبی کانولوشنال مورد استفاده قرار گیرد. به طور کلی، این موضوع منجر به پیچیدگی محساباتی کمتری می شود، چرا که ما نیازی به محاسبه بردارهای ویژه لاپلاسین را نداریم و در این حال کانولوشن به واسطه چند جمله‌ای چبیشف (Chebyshev) محاسبه می شود.

شبکه‌های گراف پیچشی (کانولونشال) (GCN)

از شناخته‌ترین استناد در مقالات مرتبط با GNN⁴ و متدوال ترین معماری مورد استفاده در برنامه های کاربردی گراف شبکه‌های کانولوشنال (GCN) می باشد. در GCN‌ها، ضریب مکانی (K-localized) ارائه شده در ChebNets بصورت ساده‌ K=1 بیان شده است.

که تغییرات زیر را پیشنهاد دادند:

آنها به واسطه جمع ماتریس همانی (یکه) I با ماتریس مجاورت A فرآیند خودپیوندی را اعمال می کنند.

A^~=A+I

آنها از نرمال‌سازی متقارن لاپلاسین L استفاده کردند.

$L\:_{norm}\:=D\:^{\frac{-1}{2}}\:\:LD\:^{\frac{-1}{2}}\:\:=I−D\:^{\frac{-1}{2}}\:\:AD\:^{\frac{-1}{2}}$

آنها از ترفند بازبهنجارش (renormalization) به منظور رفع مشکلات انفجار یا محوشدگی گرادیان استفاده کردند.

$I+D\:^{\frac{-1}{2}}\:\:AD\:^{\frac{-1}{2}}\:\:→\:D^{\sim }\:\:^{\frac{-1}{2}}\:\:\:A^{\sim }\:\:D^{\sim }\:\:^{\frac{-1}{2}}$

در اینجا D~ij ماتریس درجه گراف است. D~ij محاسبه مجدد سطری ماتریس مجاورت را به صورت D~ij=∑jA~ij انجام می دهد که درجه هر گره را تولید می کند.

بر اساس موارد بالا، اگر H ماتریس مشخصه و W ماتریس وزن قابل آموزش باشد، به طور کلی رویه به روزرسانی لایه GCN بصورت زیر انجام می شود:

$H^{(l+1)}\:=σ\left(\:D^{\sim }\:\:^{\frac{-1}{2}}\:\:\:A^{~\sim }\:\:D^{~\sim }\:\:^{\frac{-1}{2}}\:\:H^{(l)}\:W^{(l)}\:\right)$

از منظر گره، به روزرسانی می تواند به صورت زیر ارائه شود:

$h\:_{i}^{(l)}\:=σ\left(\sum_{_{i∈N\:j}}^{}\:c\:_{ij}\:Wh\:_{j}\:\right)$

جایی‌که

$c_{ij}=\frac{1}{\sqrt{\left| N_{i} \right|\left| N_{j} \right|}}$

که Ni و Njاندازه‌های مربوط به همسایگی گره‌ها هستند.

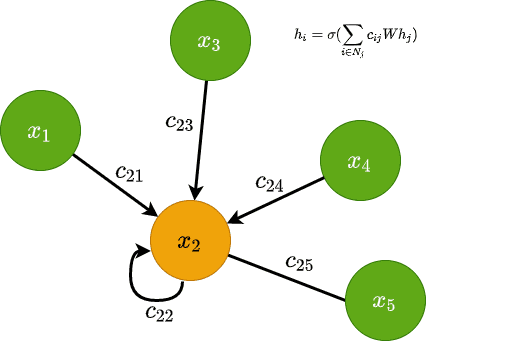
GCN‌ها از نظر محاسباتی بسیار موثر از پیشنیان خود هستند و کدنویسی آسان‌تری دارد، اما چند محدودیت دارند.

آنها بصورت مستقیم از ویژگی‌های یال پیشتیبانی نمی کنند.
آنها مفهوم پیام‌ در گراف‌ها را حذف می کنند. به طور معمول، گره‌ها می توانند پیام‌های (بردارهای عددی) را در راستای یال‌های گراف ارسال کنند.

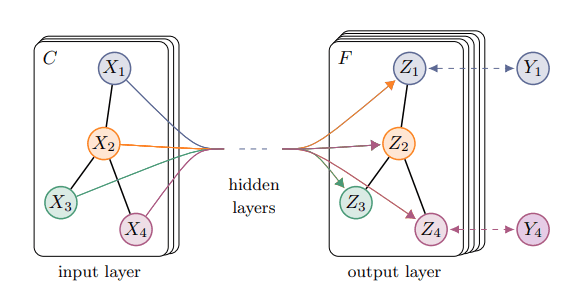
گراف شبکه کانولوشنال. منبع: طبقه بندی نیمه نظارت شده با گراف شبکه‌های کانولوشنال

متد‌های فضایی

رویکردهای فضایی مستقیما کانولوشن‌ها را به روی گراف مبتنی بر توپولوژی گراف تعریف می کند. آنها معمولا از الگو زیر پیروی می کنند:

برداری های ویژگی گره به واسطه نوعی طرح ریزی تبدیل می شود .
آنها توسط یک تابع تغیر ناپذیر جایگشتی تجمیع می گردند.
بردار ویژگی هر گره بر اساس مقادیر فعلی و تجمیع در مجاورت خود به روزرسانی می شوند.

شبکه‌های عصبی تبادل پیام (MPNN)

در اصل شبکه‌های عصبی تبادل پیام (MPNN) ⁵ از مفاهیم پیام در GNNها استفاده می کنند. یک پیام m_ij می تواند در راستای یال‌ها i و j ارسال شود و به واسطه یک تابع پیام f_e مورد محاسبه قرار می گیرد. به طور کلی f_e یک MLP کوچک و با در نظر گرفتن هر دو ویژگی گره‌ها و یال‌ها می باشد. از نظر ریاضی، برای دو گره‌های i و j با ویژگی‌های یال e_ij که در زیر رابطه زیر را داریم :

$m\:_{ij}\:=f\:_{e}\:\left(h\:_{i}\:,h\:_{j}\:,e\:_{ij}\:\right)$

سپس توسط یک تابع تغییرناپذیر جایگشتی همه پیغام‌های دریافتی در هر گره تجمیع می گردد، همانند مجموع‌یابی، سپس تجمیع به دست آمده با ویژگی‌های موجود گره f_v (MLP دیگر) ترکیب می گردد. در نتیجه مشاهده می کنیم که بردار ویژگی به روزرسانی می شود. به صورت ریاضی داریم:

$h\:_{i}\:=f\:_{v}\:\left(h\:_{i}\:,\:\:\sum_{_{j∈N\:i}}^{}\:m\:_{ji}\:\right)$

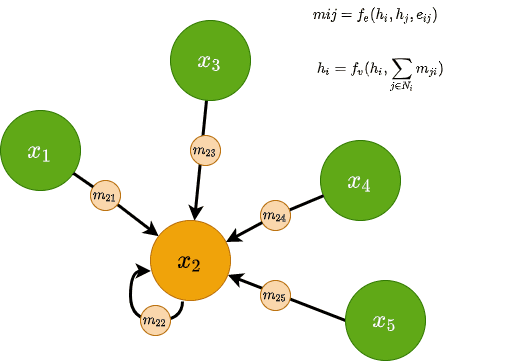
MPNN‌ها از قدرتمندترین فرمورک‌ها (چارچوب) و از متدوال ترین معماری‌های بکار رفته در GNN محسوب می شوند. هرچند مسئله مقایس‌پذیری(scalability) گاها مشکلاتی را ایجاد می کند. به چه دلیل؟ زیرا آنها نیازمند ذخیره و پردازش پیام‌های یال و همچنین ویژگی‌های گره هستند. به این دلیل است که در عمل بیشتر برای گراف های کوچک مورد استفاده قرار می گیرد.

شبکه های توجه گرافی (GAT)

قبل از شرح شبکه‌های توجه گرافی ⁶ لازم است مرور دیگر بروی رویه به روزرسانی GCNها داشته باشیم. همانطور که می دانید ما ضرایب / [\frac{1}{\sqrt{\left| N_{i} \right|\left| N_{j} \right|}}\] را داریم که در طرح ما از ویژگی‌های گره ضرب شده است. این ضرایب از ماتریس درجه گراف به دست آمده و به شدت به ساختار گراف وابسته می باشد. که در اینجا اهمیت ویژگی‌های گره j بر ویژگی‌های گره i قابل ملاحظه می باشد.

$i}^{(l)}\:=σ\left( \sum_{_{i∈N{j}}}^{{}}\frac{1}{\sqrt{\left| N_{i} \right|\left| N_{j} \right|}}Wh_{j} \right)$

ایده اصلی GAT محاسبه ضرایب به صورت ضمنی است در حالی که در GCN این مسله بصورت دقیق انجام می گیرد. به این ترتیب، می توانیم علاوه بر ساختار گراف، از اطلاعات بیشتری برای تعیین “اهمیت” هر گره استفاده کنیم. به چه صورت؟ با در نظر گرفتن ضرایب به عنوان مکانیزم قابل یادگیری توجه امکان پذیر می باشد.

بنابراین نویسندگان GAT پیشنهاد استفاده از ضریب، که از این بعد به صورت a_ij نشان داده خواهد شد، مورد محاسبه از ویژگی‌های گره را ارائه می کنند که بعدا قابل انتقال به یک تابع توجه باشد. توجه داشته باشید که می تواند شامل ویژگی‌های یال نیز باشد. در نهایت، حاصل با اعمال تابع softmax در اوزان توجه a_ij موجب توزیع احتمال می گردد.

به صورت ریاضی داریم :

$a_{ij}\:=attention\left(h_{i}\:,h_{j}\:\right)$

$a_{ij}=\frac{exp(a_{ij})}{\sum_{_{k∈Ni}}^{}exp\left(a\:_{ik}\:\right)}$

رابطه فوق را بصورت بصری در سمت چپ تصویر می توانیم مشاهده کنیم:

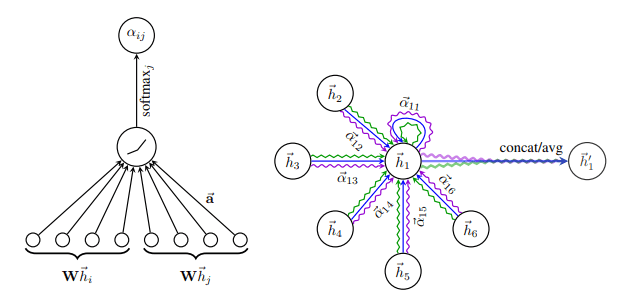
توجه در GAT. سمت چپ : مکانیزم توجه | سمت راست : تصویری از مکانیزم توجه چند سر به مجاورت خود : برگرفته از Graph Attention Networks ⁶

حال روند به روزرسانی بصورت زیر شکل می گیرد:

$h\:_{i}^{\left(l\right)\:}=σ\left(\:\sum_{i∈Nj}a\:_{ij}\:Wh\:_{j}\:\right)$

قبل از ادامه لازم است به چند نکته توجه کنید:

GATها نسبت به انتخاب تابع توجه مقاومت دارند. در این مقاله، نویسندگان از تابع امتیاز افزودنی که توسط Bahdanau و همکارانش ارائه شده است، استفاده کردند.
توجه چند سر نیز با موفقیت همراه است. همانطور که در تصویر راست بالا نشان داده شده است، آنها به طور همزمان K=3 سر توجه متنوع را محاسبه و سپس به منظور ایجاد بردار ویژگی جدید، ویژگی ها موجود را به هم دیگر متصل می کنند.
ضریب به ساختار گراف وابسته نبوده و فقط از طرز نمایش آن متاثر می باشد.
از نظر محاسباتی GATها بسیار کارآمد ظاهر می شوند.
فرآیند را به منظور شمول ویژگی‌های یال می توان توسعه داد.
آنها کاملا مقایس‌پذیر هستند.

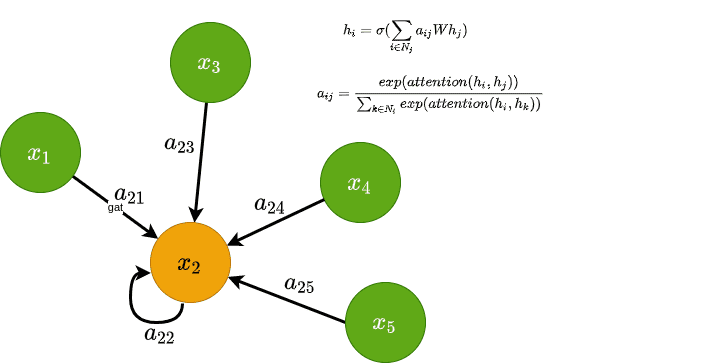
متدهای نمونه‌ برداری

یکی از معایب بزرگ معماری‌های GNN مقایس پذیری است. به طور کلی، هر بردار ویژگی گره به همه مجاورت خود وابسته می باشد که این می تواند برای گراف‌های عظیم با مجاورت‌های بزرگ کاملا ناکارآمد ظاهر شود. برای حل این مسئله، ماژول‌های نمونه برداری گنجانده شده است. ایده اصلی ماژول‌های نمونه برداری به این صورت است که به جای استفاده از همه اطلاعات مجاور (همسایگی)، می توانیم از زیر مجموعه آنها به منظور انتشار نمونه برداری داشته باشیم.

GraphSage

GraphSage ⁷ با پیشنهاد استفاده از فرمورک(چارچوب) زیر این ایده را متدوال ساخت :

به طرز یکنواخت، مجموعه ای از گره ها را از همسایگی نمونه برداری کنید.
اطلاعات مربوط به ویژگی را از همسایگان نمونه، جمع آوری کنید.
بر اساس تجمیع، طبقه بندی گراف یا طبقه بندی گره را انجام دهید.

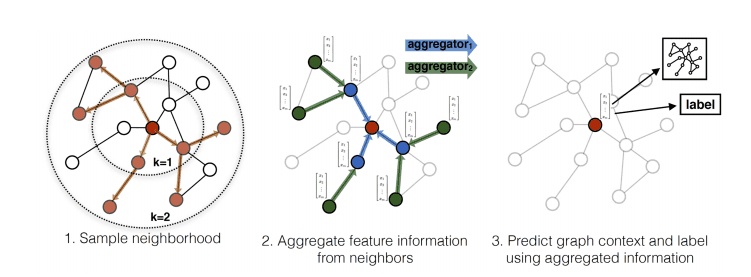
فرآیند GraphSage. منبع: آموزش بازنمایی استقرایی روی گراف‌های بزرگ ⁷

در هر لایه، ما عمق همسایگی K را گسترش می دهیم که منجر به نمونه برداری از ویژگی های گره K-hops دور می شود. این موضوع شبیه به افزایش میدان پذیرش در شبکه‌های کلاسیک می باشد. قابل ملاحظه است که این موضوع در قیاس با رویه استفاده از همه همسایگی (مجاروت) چقدر می تواند از نظر محاسبانی کار آمد واقع گردد و منجر به انشتار رو به رشد GraphSage شود.

با این وجود، مشارکت کلیدی مقاله GraphSage در تشریح چگونگی آموزش واقعی مدل بوده است. در این خصوص نویسندگان دو ایده پایه ای را مطرح کردند:

مدل را کاملا به روش فاقد نظارت آموزش دهید. می توانیم به واسطه یک تابع زیان که گره‌های همسایه را مجبور به ارائه مشابه و گره‌های متمایز را مجبور به ارائه متمائز می کند، انجام دهید.
می توانیم از روش نظارت بر آموزش به واسطه برچسب‌ها و یک شکل از آنتروپی متقاطع برای یادگیری ارائه گره‌ها استفاده کنیم.

بخش مشکل ساز این موضوع این است که ما همچنین تابع تجمیع را در کنار ماتریس‎های وزن قابل آموزش مان، آموزش می دهیم. نویسندگان با سه تابع تجمیع مختلف مورد آزمایش قرار دادند: الف) یک جمع کننده میانگین ب) یک جمع کننده LSTM و ج) یک جمع کننده حداکثر تجمع، در هر سه مورد ذکر شده، توابع شامل پارامترهای قابل آموزش هستند که در طول برنامه آموزش داده می شوند. به این ترتیب شبکه روش “صحیح” را به خود آموزش می دهد تا ویژگی‌های لازم را از گره‌های نمونه برداری شده کسب کند.

PinSAGE

PinSAGE⁸ یک دنباله روی مستقیم از GraphSAGE می باشد که یکی از محبوب‌ترین برنامه GNNها محسوب می گردد. در اصل PinSAGE بر پایه GraphSAGE است که در گراف بزرگ ( سه میلیارد گره و 18 میلیارد یال) اعمال می شود. PinSAGE توسط Pinterest معرفی شده و در سیستم توصیه (پیشنهادی) خود نیز از آن بهره برده‌اند.

در کنار عملکرد مهندسی فوق‌العاده که بخش بزرگی از مقاله را برمی گیرد، ما قصد داریم در اینجا به آن نپردازیم اما بصورت مختصر اصول اساسی معماری آن را تشریح می کنیم:

آنها همسایگی گره را به واسطه گام‌های تصادفی تعریف می کنند و در ادامه با شبیه سازی گام‌های تصادفی که از گره‌های هدف شروع می شود و حتی می توانند گره‌های بالا (top nodes) با بیشترین تعداد بازدید را مورد انتخاب قرار دهند. یکی از اثر جانبی این موضوع، اختصاص امتیاز اهمیت به هر گره که نشان دهنده میزان اهمیت آن برای گره هدف است، می باشد.
تجمیع با استفاده از “نمونه برداری اَهم ” صورت می گیرد. در نمونه برداری اَهم، به سادگی امتیاز‌های اَهم ایجاد شده توسط گام‌های تصادفی را نرمالیزه و جمع‌بندی می کنیم.
مدل به سبک نظارت به روی یک مجموعه داده‌ها از گره‌ها که بر اساس تعامل گذشته کاربران در نرم افزار Pinterest به یکدیگر متصل شده، آموزش دیده‌اند.

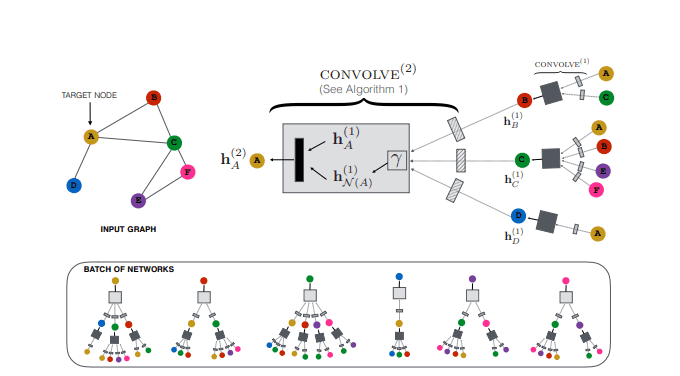
نمای کلی PinSAGE. منبع: Graph Convolutional Neural Networks for Web-Scale Recommender Systems⁸

گراف‌های پویا (داینامیک)

گراف‌های پویا، گراف‌های هستند که ساختار آنها در طول زمان تغییر می کند. این تغییر شامل هر دو گره‌ و یال‌ می شود که امکان اضافه، اصلاح و حذف را دارند. برای مثال، به شبکه‌های اجتماعی، تراکنش‌های مالی و موارد دیگر اشاره کرد. یک گراف پویا می تواند به عنوان یک فهرست مرتب شده یا یک جریانی از رویدادهای دارای مشخصه زمانی که ساختار گراف را مورد تغییر قرار می دهند، ارائه شود.

تحقیقات یادگیری ماشین (ML) به روی گراف‌های پویا بسیار جدید است. با این وجود چند معماری قابل ملاحظه‌ای در این زمینه وجود دارد.

شبکه های گراف زمانی (TGN)

شبکه‌های گراف زمانی ⁹ نویدبخش ‌ترین معماری است. از آنجا که گراف‌های پویا به عنوان یک لیست زمان‌بندی ارائه می شود، همسایگی‌های گره در طول زمان تغییر می کند. در هر زمان t می توانیم تصویر لحظه‌ای را از گراف دریافت کنیم. همسایگی (مجاورت) موجود در یک زمان خاص t را یک همسایگی زمانی می نامند.

همانطور که در تصویر زیر مشاهده می کنید، هدف TGN پیش بنی لازم برای تعبیه گره‌ها در یک برچسب زمانی مشخص می باشد. این تعبیه‌ها را می توان به عنوان ورودی به یک شبکه رمزگشا (Decoder) اعمال کرد تا بصورت تکلیف در دست اقدام اجرا کند.

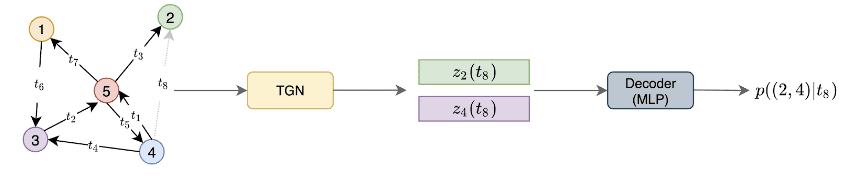
نمونه ای از رمزگذار TGN در یک گراف پویا . منبع: یادگیری عمیق بر روی گراف‌های پویا توسط امانوئل روسی و مایکل برونشتاین (Emanuele Rossi and Michael Bronstein)

این معماری توسط توئیتر (Twitter) مطرح شده و به روی گراف تئویت‌ها آموزش داده شده است. گره‎ها نشاندهنده توئیت‌ها و یال‌ها تعامل بین آنها می باشد. هدف مدل پیش بینی تعاملاتی است که در برچسب زمانی t به شکل احتمال، اتفاق نیافتاده است. به عبارت دیگر، یک پیش بینی یال انجام داده‌اند. این شبکه به روش خود نظارت (self-supervised) آموزش داده می شوند: در طول هر دوره، فرآیند رمزگذار رویدادها را به ترتیب زمانی پردازش می کند و تعامل بعدی را بر اساس موارد قبلی پیش بینی می کند.

اما رمزگذار TGN دقیقاً چگونه به نظر می رسد؟

شبکه GAT جزوء مولفه اصلی شبکه است که تعبیه گره‌ها را ارائه می کند. ماژول GAT اطلاعات را به دو صورت دریافت می کند:

ویژگی گره‌های مجاور زمانی در یک زمان خاص، ما به راحتی ویژگی‌ها را از مجاورت به ماژول GAT منتقل می کنیم که آنها تبدیل (دگرگون)، تجمیع، و به روزرسانی نهان ارائه خواهند شد.
حافظه گره، حافظه گره یک نمایش فشرده از تعاملات گذشته گره می باشد. هر گره نمایش متفاوتی نسبت به هر برچسب زمانی را دارند. همانطور که در MPNNها شرح دادیم، حافظه به واسطه پیام‌ها به روزرسانی می شوند. همه پیام‌های گره متنوع توسط ماژول حافظه که معمولا بصورت شبکه عصبی بازگشتی (RNN) پیاده‌سازی می شود، تجمیع و پردازش می گردد.

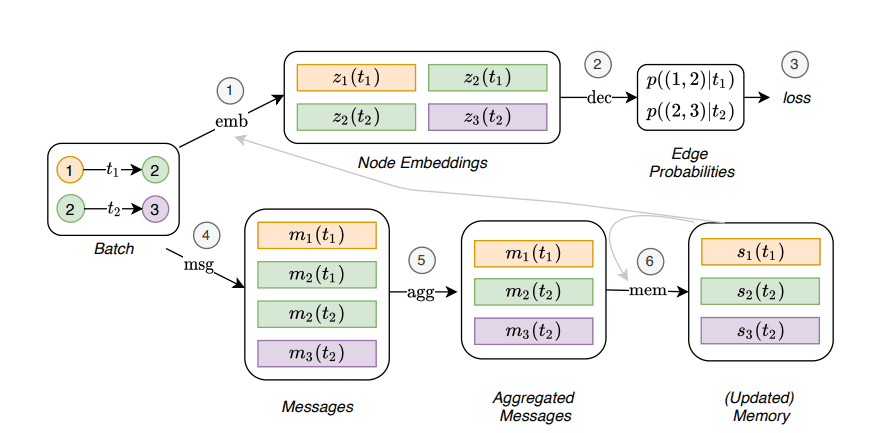
شبکه گراف زمانی منبع: Temporal Graph Networks for Deep Learning on Dynamic Graphs ⁹

نتیجه‌گیری

GNNها حوزه تحقیقاتی فعال، به روز و با ظرفیت بسیار بالای هستند. چرا که در برنامه های کاربردی روزمره مجموعه داده‌های متنوعی وجود دارد که می توانیم بصورت گراف ساختاریافته باشند. در دوره آموزشی شکه عصبی گراف ، ما از Pytorch Geometric برای کار با گراف‌ها و ساختن GNN خودمان استفاده خواهیم کرد.

دوره‌ی آموزشی ویدیویی Graph Neural Network

علاوه بر آن میتوانید به پست معرفی منابع شبکه های عصبی گراف نیز مراجعه کنید.

در انتها خواهشمندیم برای ارتقاء کیفیت مطالب، نظرات و پیشنهادات خودتان را با ما در میان بگذارید و با خرید دوره حامی ما باشید.

منبع اصلی:

https://theaisummer.com/gnn-architectures/