خودرمزگذار متغیر یا VAE چیست و چگونه کار می‌کند؟

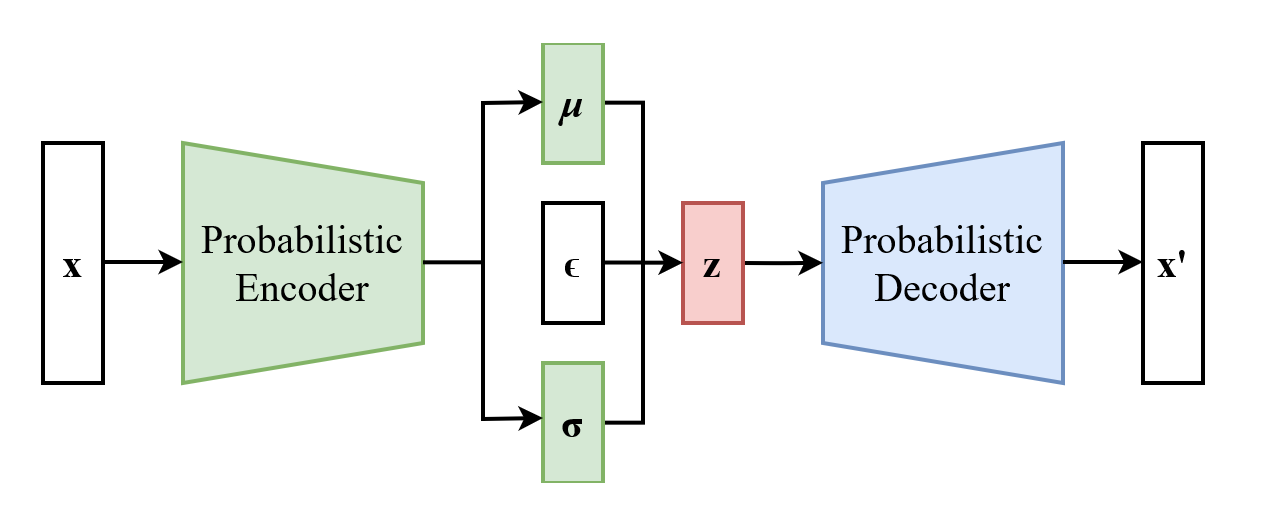
چگونگی عملکرد خودرمزگذار متغیر (Variational Autoencoder یا VAE):

قبلا پیرامون خودرمزگذار یا اتو-انکودر خوانده ایم.

آنچه خودرمزگذار متغیر (VAE) را از سایر خودرمزگذارها متمایز می‌کند، نحوه خاص کدگذاری فضای نهان (Latent Space) و استفاده‌های متفاوت از این کدگذاری احتمالاتی است.

برخلاف بیشتر خودرمزگذارها که مدل‌های قطعی (Deterministic Models) هستند و یک بردار منفرد از متغیرهای نهانی گسسته (Discrete Latent Variables) را کد می‌کنند، خودرمزگذارهای متغیر مدل‌های احتمالاتی (Probabilistic Models) هستند. آن‌ها متغیرهای نهان داده‌های آموزشی را به‌صورت یک مقدار ثابت گسسته کد نمی‌کنند، بلکه آن‌ها را به شکل طیفی پیوسته از احتمالات (Continuous Range of Possibilities)، که به‌صورت توزیع احتمالی (Probability Distribution) نمایش داده می‌شود، کد می‌کنند.

در آمار بیزی (Bayesian Statistics)، این طیف احتمالات برای متغیر نهانی، توزیع پیشین ( $\text{Prior Distribution}$ ) نامیده می‌شود. در استنتاج تغییراتی( $\text{Variational Inference}$ )، که بخشی از فرآیند تولید داده‌های جدید ( $\text{Generative Process}$ ) است، این توزیع پیشین برای محاسبه توزیع پسین ( $\text{Posterior Distribution}$ ) استفاده می‌شود، $p(z \mid x)$ . به‌عبارت دیگر، این نشان‌دهنده احتمال متغیرهای قابل مشاهده ( $x$ ) با توجه به یک مقدار مشخص برای متغیر نهانی ( $z$ ) است.

برای هر ویژگی نهان داده‌های آموزشی، خودرمزگذار متغیر(VAE) دو بردار متفاوت را کد می‌کند: یک بردار از میانگین‌ها (“μ”) و یک بردار از انحراف معیارها (“σ”). در اصل، این دو بردار نشان‌دهنده طیف احتمالات برای هر متغیر نهانی و میزان تغییرات مورد انتظار در هر طیف احتمالات هستند.

با نمونه‌برداری تصادفی از این طیف احتمالات کدشده، خودرمزگذار متغیر می‌تواند نمونه‌های جدیدی ایجاد کند که در عین منحصربه‌فرد بودن، شباهت قابل توجهی به داده‌های آموزشی اصلی دارند. اگرچه این روش در اصول به‌ظاهر ساده به نظر می‌رسد، اما برای به‌کارگیری آن در عمل، نیاز به تغییرات بیشتری در معماری استاندارد خودرمزگذار دارد.

برای توضیح این توانایی در خودرمزگذار متغیر، مفاهیم زیر را بررسی خواهیم کرد:

خطای بازسازی (Reconstruction Loss)
واگرایی کولبک-لیبلر (Kullback-Leibler Divergence یا KL Divergence)
کران پایین شواهد (Evidence Lower Bound یا ELBO)
ترفند بازپارامتردهی (Reparameterization Trick)

خطای بازسازی (Reconstruction Loss)

مانند تمام خودرمزگذارها، خودرمزگذار متغیر از خطای بازسازی یا خطای بازتولید (Reconstruction Error) به‌عنوان تابع خطای اصلی در آموزش استفاده می‌کند. خطای بازسازی بین داده ورودی اصلی و نسخه بازسازی‌شده آن توسط بخش رمزگشا (Decoder) یا به عبارتی تفاوت ورودی/ خروجی را اندازه‌گیری می‌کند. الگوریتم‌های مختلفی مانند Cross-Entropy یا میانگین مربع خطا (Mean-Squared Error یا MSE) می‌توانند به‌عنوان تابع خطای بازسازی استفاده گردد.

همان‌طور که پیش‌تر توضیح داده شد، معماری خودرمزگذار یک گلوگاه (Bottleneck) ایجاد می‌کند که تنها بخشی از داده‌های ورودی اصلی را اجازه عبور به رمزگشا می‌دهد. در ابتدای آموزش، که معمولاً با یک مقداردهی اولیه تصادفی (Random Initialization) برای پارامترهای مدل آغاز می‌شود، بخش رمزگذار (Encoder) هنوز نیاموخته است که کدام بخش از داده‌ها را باید بیشتر در نظر بگیرد. بنابراین، در ابتدا یک نمایش نهان نامطلوب (Suboptimal Latent Representation) ارائه می‌دهد و بخش رمزگشا بازسازی ناقص یا نادقیقی از ورودی اصلی را ارائه خواهد داد.

با کاهش خطای بازسازی از طریق Gradient Descent بر پارامترهای شبکه رمزگذار و رمزگشا، وزن‌های مدل خودرمزگذار به‌گونه‌ای تنظیم می‌شوند که یک کدگذاری مفیدتر از فضای نهانی ایجاد کنند و در نتیجه، بازسازی دقیق‌تری انجام دهند. به‌طور ریاضی، هدف تابع خطای بازسازی، بهینه‌سازی $p_\theta(x \mid z)$ است، که در آن $\theta$ نمایانگر پارامترهای مدلی است که بازسازی دقیق ورودی $x$ را با توجه به متغیر نهانی $z$ تضمین می‌کند.

خطای بازسازی به‌تنهایی برای بهینه‌سازی اکثر خودرمزگذارها کافی است، زیرا هدف اصلی آن‌ها یادگیری یک نمایش فشرده از داده‌های ورودی است که به بازسازی دقیق منجر شود.

اما هدف یک خودرمزگذار متغیر، بازسازی ورودی اصلی نیست؛ بلکه ایجاد نمونه‌های جدیدی است که به ورودی اصلی شباهت دارند. بنابراین، یک عبارت بهینه‌سازی اضافی مورد نیاز است.

واگرایی کولبک-لیبلر (Kullback-Leibler Divergence یا KL Divergence)

برای اهداف استنتاج تغییراتی( $\text{Variational Inference}$ )—یعنی تولید نمونه‌های جدید توسط یک مدل آموزش‌دیده—خطای بازسازی به‌تنهایی می‌تواند به یک کدگذاری نامنظم از فضای نهانی منجر شود که داده‌های آموزشی را بیش از حد می‌آموزد (Overfitting) و در تولید نمونه‌های جدید ضعیف عمل می‌کند. از این رو، خودرمزگذار متغیر یک عبارت رگیولاریزیشن(regularization) دیگر را نیز اضافه می‌کند: واگرایی کولبک-لیبلر با به اختصار KL divergence!

برای تولید تصاویر، رمزگشا از فضای نهانی نمونه‌برداری می‌کند. نمونه‌برداری از نقاط خاصی در فضای نهانی که ورودی‌های اصلی داده‌های آموزشی را نشان می‌دهند، همان ورودی‌های اصلی را تکرار می‌کند. برای تولید تصاویر جدید، خودرمزگذار متغیر باید بتواند از هر نقطه در فضای نهانی بین داده‌های اصلی نمونه‌برداری کند. برای این کار، فضای نهانی باید دو نوع نظم را داشته باشد:

پیوستگی (Continuity): نقاط نزدیک در فضای نهانی باید هنگام رمزگشایی محتوای مشابهی ایجاد کنند.
کامل بودن (Completeness): هر نقطه‌ای که از فضای نهانی نمونه‌برداری شود، باید هنگام رمزگشایی محتوای معناداری تولید کند.

یک روش ساده برای اعمال هر دو ویژگی پیوستگی و کامل بودن در فضای نهان(latent space) این است که مطمئن شویم فضای نهانی از یک توزیع نرمال استاندارد (Standard Normal Distribution) پیروی می‌کند. اما بهینه‌سازی تنها خطای بازسازی، مدل را به سازماندهی خاصی از فضای نهانی وادار نمی‌کند، زیرا فضای “میانی” برای بازسازی دقیق داده‌های اصلی چندان مهم نیست. در اینجا است که KL divergence وارد عمل می‌شود.

واگرایی کولبک-لیبلر (KL Divergence) معیاری برای مقایسه دو توزیع احتمالی است. به حداقل رساندن KL divergence بین توزیع یادگرفته‌شده برای متغیرهای نهان و یک توزیع گاوسی ساده (Gaussian Distribution) با مقادیر استاندارد، باعث می‌شود کدگذاری یادگرفته‌شده از متغیرهای نهانی به شکل توزیع نرمال درآید. این کار اجازه می‌دهد که هر نقطه‌ای در فضای نهانی به شکلی پیوسته و روان به محتواهای جدید تبدیل شود و به همین دلیل تولید نمونه‌های جدید ممکن گردد.

کران پایین شواهد (Evidence Lower Bound یا ELBO)

یکی از چالش‌های استفاده از KL divergence برای استنتاج متغیر این است که مخرج این معادله غیرقابل محاسبه است، به این معنا که محاسبه آن به زمان نظری بی‌نهایت نیاز دارد. برای حل این مشکل و ترکیب هر دو تابع خطای کلیدی، خودرمزگذارهای متغیر با به جای حداقل‌سازی KL divergence، کران پایین شواهد (ELBO) را حداکثر می‌کنند.

در اصطلاحات آماری، “شواهد” (evidence) در عبارت کران پایین شواهد (Evidence Lower Bound – ELBO) به ورودی‌های قابل مشاهده $p(x)$ اشاره دارد؛ یعنی همان داده‌های ورودی که خودرمزگذار متغیر (Variational Autoencoder) مسئول بازسازی آن‌ها است. این متغیرهای قابل مشاهده در داده‌های ورودی، “شواهد” (evidence) هستند که متغیرهای نهانی (latent variables) کشف‌شده توسط خودرمزگذار را توجیه می‌کنند. منظور از “کران پایین” (lower bound) نیز بدترین حالت ممکن برای تخمین log-likelihood یک توزیع مشخص است. احتمال واقعی ممکن است بیشتر از مقدار کران پایین شواهد (ELBO) باشد.

در زمینه خودرمزگذارهای متغیر، کران پایین شواهد به بدترین حالت ممکن از احتمال مطابقت یک توزیع پسین خاص(posterior distribution)—یعنی خروجی خاصی از خودرمزگذار که تحت تأثیر عبارت‌های خطای واگرایی KL و خطای بازسازی قرار گرفته است—با “شواهد” موجود در داده‌های آموزشی اشاره دارد. از این رو، آموزش یک مدل برای استنتاج متغیر را می‌توان به‌صورت حداکثرسازی ELBO در نظر گرفت.

ترفند بازپارامتردهی (Reparameterization Trick)

همان‌طور که بحث شد، هدف استنتاج متغیر(Variational Inference) تولید داده‌های جدید به‌صورت تغییرات تصادفی از داده‌های آموزشی $x$ است. در نگاه اول، این کار نسبتاً ساده به نظر می‌رسد: استفاده از یک تابع $f$ که یک مقدار تصادفی برای متغیر نهانی $z$ انتخاب کند و سپس رمزگشا از این مقدار برای تولید یک بازسازی تقریبی از $x$ استفاده کند.

اما یکی از ویژگی‌های ذاتی تصادفی بودن این است که نمی‌توان آن را بهینه‌سازی کرد. هیچ “بهترین” مقدار تصادفی وجود ندارد؛ یک بردار از مقادیر تصادفی، به‌تعریف، مشتق‌پذیر نیست—یعنی هیچ گرادیانی وجود ندارد که الگویی در خروجی‌های مدل را نمایش دهد—و بنابراین نمی‌توان آن را با روش‌های متداول مانند پس‌انتشار خطا (Backpropagation) و هر نوع Gradient Descent بهینه‌سازی کرد. این بدان معناست که یک شبکه عصبی که از فرایند نمونه‌برداری تصادفی فوق استفاده می‌کند، قادر به یادگیری پارامترهای بهینه برای انجام وظیفه خود نخواهد بود.

برای غلبه بر این مشکل، Variational Autoencoderها از ترفند بازپارامتردهی (Reparameterization Trick) استفاده می‌کنند. این ترفند یک پارامتر جدید به نام $\epsilon$ را معرفی می‌کند که یک مقدار تصادفی انتخاب‌شده از توزیع نرمال استاندارد (Standard Normal Distribution) بین 0 و 1 است.

سپس متغیر نهانی $z$ را به‌صورت $z = \mu_x + \epsilon\sigma_x$ بازپارامتردهی می‌کند. به‌زبان ساده، این روش مقداری را برای متغیر نهانی $z$ با شروع از میانگین آن (که با $\mu$ نمایش داده می‌شود) و تغییر دادن آن به میزان چندبرابر تصادفی از یک انحراف معیار ( $\sigma$ )، انتخاب می‌کند. رمزگشا با توجه به این مقدار خاص از $z$ ، یک نمونه جدید تولید می‌کند.

از آنجا که مقدار تصادفی $\epsilon$ از پارامترهای مدل مستقل است و هیچ ارتباطی با پارامترهای خودرمزگذار ندارد، می‌توان آن را در هنگام پس‌انتشار خطا نادیده گرفت. مدل از طریق یکی از روش‌های نزول گرادیان—که معمولاً الگوریتم Adam (مقاله adam) است—به‌روزرسانی می‌شود تا کران پایین شواهد(ELBO) را به حداکثر برساند.

خلاصه

خودرمزگذارهای متغیر (VAEs) ابزارهای قدرتمندی برای مدل‌سازی داده‌ها هستند که از ساختار خاصی برای پردازش و تولید داده‌های جدید استفاده می‌کنند. این روش‌ها با استفاده از یک رویکرد احتمالی به جای روش‌های تعیین‌شده، به گونه‌ای طراحی شده‌اند که فضای نهانی را به شکلی سازمان‌دهی شده و معنی‌دار شکل دهند.

فضای نهانی: در خودرمزگذارهای متغیر، فضای نهانی به‌صورت یک توزیع پیوسته مدل‌سازی می‌شود که به مدل اجازه می‌دهد تا نمونه‌های جدیدی تولید کند که مشابه داده‌های آموزشی هستند، اما هرگز دقیقاً مشابه آن‌ها نیستند. این امر به مدلسازان این امکان را می‌دهد که به‌راحتی بین نمونه‌های مختلف حرکت کنند و نتایج نوآورانه‌ای تولید کنند.
بهینه‌سازی: با ترکیب دو تابع خطا—خطای بازسازی و واگرایی KL—VAEs می‌توانند داده‌ها را به‌گونه‌ای بهینه کنند که هم کیفیت بازسازی و هم قابلیت تولید نمونه‌های جدید را بهبود ببخشند. این رویکرد به خودرمزگذارها این امکان را می‌دهد که ویژگی‌های خاصی از داده‌ها را یاد بگیرند و در عین حال، فضای نهانی را در حداقل حالت ممکن نگه‌دارند.
کاربردها: خودرمزگذارهای متغیر در بسیاری از حوزه‌ها مانند تولید تصویر، پردازش زبان طبیعی و تحلیل داده‌های بزرگ مورد استفاده قرار می‌گیرند. آن‌ها می‌توانند به‌عنوان ابزاری برای کشف ساختار در داده‌های پیچیده عمل کنند و برای تولید محتواهای جدید و جالب به کار گرفته شوند.
چالش‌ها: علی‌رغم مزایای فراوان VAEs، چالش‌هایی نیز وجود دارد، از جمله نیاز به ترفندهای خاص برای بهینه‌سازی و مدیریت داده‌های پیچیده. همچنین، ساختار مدل باید به‌گونه‌ای طراحی شود که از تناقض‌های احتمالی جلوگیری کند و به بهترین نحو عملکرد بهینه را به دست آورد.