همه چیز درباره توابع فعالیت (Activation Functions) در شبکه‌های عصبی و مشکل محو شدگی گرادیان

در دنیای یادگیری عمیق و شبکه‌های عصبی، توابع فعالیت (Activation Functions) نقش بسیار مهمی در تعیین عملکرد و دقت مدل‌های هوش مصنوعی دارند. این توابع کمک می‌کنند تا شبکه‌های عصبی غیرخطی شوند و قادر باشند الگوهای پیچیده‌تری را یاد بگیرند. در این مقاله، به بررسی انواع توابع فعالیت، ویژگی‌ها و کاربردهای آنها می‌پردازیم.

تعریف تابع فعالیت

تابع فعالیت یا Activation Function، تابعی است که در شبکه عصبی به کار می‌رود و ورودی یک نورون را به یک خروجی غیرخطی تبدیل می‌کند. این خروجی معمولاً در یک محدوده خاص قرار می‌گیرد (مانند [0, 1] یا [-1, 1]). توابع فعالیت دو هدف اصلی را دنبال می‌کنند: اول، می‌توانند سطح فعالیت نورون‌ها را تنظیم کنند، به عنوان مثال، در لایه آخر شبکه برای تبدیل خروجی‌های نورون‌ها به احتمال‌های دسته‌بندی (در مسائل طبقه‌بندی). دوم، با افزودن غیرخطی‌سازی به لایه‌های میانی، امکان یادگیری الگوهای پیچیده‌تر را برای شبکه عصبی فراهم می‌کنند که به بهبود دقت و کارایی مدل کمک می‌کند.

چرا تابع فعالیت مهم است؟

توابع فعالیت به چند دلیل کلیدی در شبکه‌های عصبی مورد استفاده قرار می‌گیرند:

غیرخطی بودن: در صورتی که از توابع خطی استفاده کنیم، شبکه عصبی نمی‌تواند الگوهای پیچیده را یاد بگیرد. توابع فعالیت غیرخطی مانند ReLU یا Sigmoid این مشکل را حل می‌کنند. صدالبته معمولا ReLU گزینه بهتری نسبت به Sigmoid و Tanh است.
کمک به یادگیری عمیق: توابع فعالیت اجازه می‌دهند تا شبکه‌های عصبی چندین لایه عمیق داشته باشند، که این امر باعث می‌شود مدل‌ها قدرت بیشتری در شناسایی الگوهای پیچیده داشته باشند. اگر ما چند واحد خطی را ترکیب کنیم باز تابع خروجی خطی است، اما اگر چند واحد غیر خط را ترکیب کنیم، حاصل یک غیر خطی پیچیده تر خواهد بود.
پیشگیری از مشکلات محو شدگی گرادیان : انتخاب تابع فعالیت تأثیر زیادی بر آموزش شبکه عصبی دارد. به عنوان مثال، قبل از سال‌های 2008 تا 2012، از توابعی نظیر Sigmoid و Tanh در لایه‌های میانی استفاده می‌شد. اما این توابع به دلیل خاصیتشان، خطر محو شدگی گرادیان (Vanishing Gradient) را افزایش می‌دادند. با معرفی تابع ReLU در سال 2008 و استفاده از آن در مقاله مشهور الکس‌نت (AlexNet) در سال 2012، این مشکل تا حد زیادی حل شد. این تغییر کوچک امکان ساخت شبکه‌های عمیق‌تر را فراهم کرد و بهبود چشمگیری در عملکرد مدل‌ها به وجود آورد.

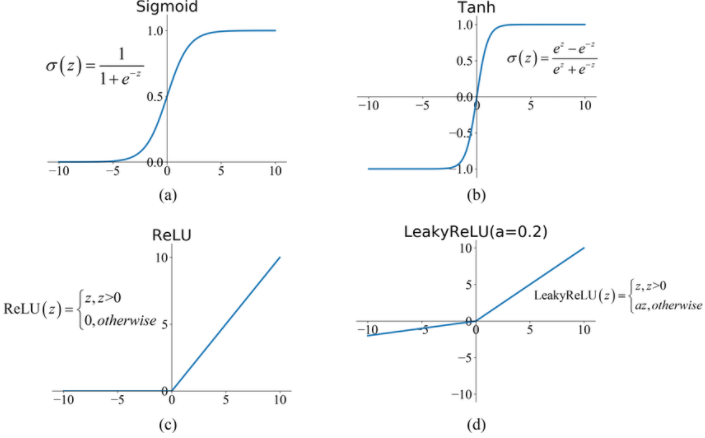
چرا Sigmoid مشکل محو شدگی گرادیان دارد؟

گرادیان نزولی (Gradient Descent) نیاز به محاسبه مشتق تابع هزینه نسبت به وزن‌ها و بایاس‌ها دارد. برای انجام این کار، باید از قانون زنجیره‌ای استفاده کنیم، زیرا مشتقی که باید محاسبه کنیم ترکیبی از دو تابع است. طبق قانون زنجیره‌ای، باید مشتق تابع سیگموید را محاسبه کنیم. یکی از دلایلی که تابع سیگموید به عنوان تابع فعالیت در شبکه‌های عصبی محبوب است، این است که مشتق آن به راحتی قابل محاسبه است.

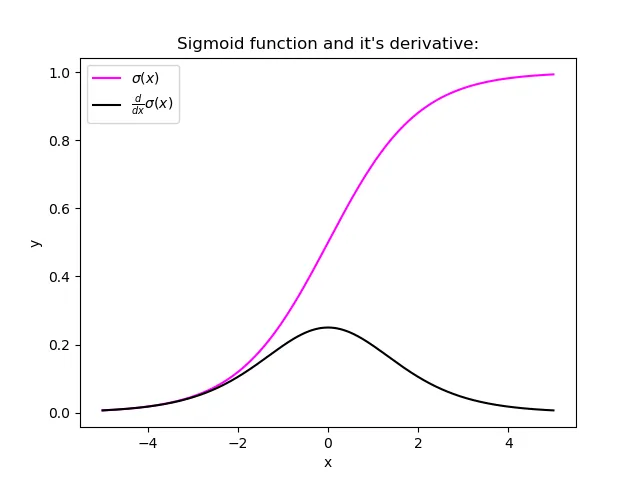
اما اگر به شکل بالا نگاه کنید، متوجه می‌شوید که مشتق تابع سیگموید در انتهای تابع (یعنی زمانی که ورودی بزرگ و مثبت یا منفی است) به اشباع می‌رسد و مقادیر مشتق نزدیک به صفر هستند. در هر مرحله، زمانی که خطا به شبکه بازگردانده می‌شود، لایه قبلی با مقدار مشتق کوچک‌تر ضرب می‌شود، بنابراین مشتق به تدریج به صفر نزدیک می‌شود. این همان دلیلی است که باعث می‌شود گرادیان‌ها در نزدیکی لایه‌های ورودی محو شوند. Tanh هم شکلی مشابه دارد و با همین مشکل مواجه است. اما اگر به شکل ReLU نگاه کنید خواهید دید که در قسمت مثبت مشتق یک داریم که جلوی این مشکل را می‌گیرد.

انواع توابع فعالی

در زیر به بررسی رایج‌ترین توابع فعالیت مورد استفاده در شبکه‌های عصبی می‌پردازیم:

1. Sigmoid

تابع Sigmoid یکی از قدیمی‌ترین و پرکاربردترین توابع فعالیت است. خروجی این تابع بین 0 و 1 قرار دارد و فرمول آن به شکل زیر است:

$\sigma(x) = \frac{1}{1 + e^{-x}}$

ویژگی‌ها:

مناسب برای خروجی‌های دودویی.
مشکل گرادیان ناپدید شونده به خصوص در لایه‌های عمیق.

کاربرد: معمولاً در لایه‌های خروجی برای مسائل دسته‌بندی دودویی مورد استفاده قرار می‌گیرد. این تابع قبل سالهای 2008 و 2012 به عنوان تابع فعالیت لایه های میانی نیز استفاده میشد که مشکل محو شدگی گرادیان را داشت.

2. ReLU (Rectified Linear Unit)

تابع ReLU یکی از محبوب‌ترین توابع فعالیت در سال‌های اخیر است. این تابع تنها زمانی که ورودی مثبت باشد فعال می‌شود و برای مقادیر منفی خروجی صفر می‌دهد:

$\text{ReLU}(x) = \max(0, x)$

ویژگی‌ها:

سادگی در پیاده‌سازی.
حل مشکل محو شدگی گرادیان .
احتمال مشکل “مرگ نورون” (Dead Neuron) در صورتی که ورودی همیشه منفی باشد.

کاربرد: به طور گسترده در لایه‌های مخفی شبکه‌های عصبی عمیق استفاده می‌شود.

3. Leaky ReLU

تابع Leaky ReLU یک تغییر جزئی از ReLU است که مشکل مرگ نورون را کاهش می‌دهد. این تابع برای ورودی‌های منفی مقدار کوچکی از شیب را نگه می‌دارد:

$\text{Leaky~ReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}$

ویژگی‌ها:

کاهش مشکل مرگ نورون.
حفظ سادگی و سرعت ReLU.

کاربرد: مشابه ReLU، در لایه‌های مخفی استفاده می‌شود، با این تفاوت که برای ورودی‌های دارای مقادیر منفی بهتر عمل می‌کند.

4. Tanh (Hyperbolic Tangent)

تابع Tanh نسخه‌ای تغییر یافته از Sigmoid است که خروجی آن بین -1 و 1 قرار دارد:

$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

ویژگی‌ها:

خروجی متمرکزتر و دارای مقدار میانی صفر.
مشابه Sigmoid، با مشکل محو شدگی گرادیان مواجه است.

کاربرد: معمولاً در لایه‌های میانی( مخفی) شبکه‌های عصبی استفاده می‌شود.

5. Softmax

تابع Softmax برای دسته‌بندی چندکلاسه استفاده می‌شود. این تابع مجموعه‌ای از خروجی‌ها را به احتمال‌های بین 0 و 1 تبدیل می‌کند که مجموع آنها برابر 1 است.

$\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}$

ویژگی‌ها:

مناسب برای خروجی‌های چندکلاسه.
امکان تفسیر خروجی به عنوان احتمال دسته‌بندی.

کاربرد: در لایه‌های خروجی شبکه‌های دسته‌بندی چندکلاسه استفاده می‌شود.

نحوه انتخاب تابع فعالیت مناسب

انتخاب تابع فعالیت مناسب بستگی به نوع مسئله، معماری شبکه عصبی و داده‌ها دارد. در زیر به چند نکته برای انتخاب تابع فعالیت مناسب اشاره می‌کنیم:

برای مسائل دسته‌بندی دودویی: تابع Sigmoid در لایه خروجی.
برای دسته‌بندی چندکلاسه: تابع Softmax در لایه خروجی.
برای لایه‌های مخفی: تابع ReLU یا نسخه‌های اصلاح‌شده آن مانند Leaky ReLU.
برای شبکه‌های بازگشتی: Tanh یا Sigmoid، اما با توجه به مشکلات گرادیان ناپدید شونده، ممکن است نیاز به استفاده از تکنیک‌هایی مانند LSTM یا GRU باشد.

جمع‌بندی

توابع فعالیت نقش اساسی در شبکه‌های عصبی ایفا می‌کنند و انتخاب مناسب آنها می‌تواند تاثیر زیادی بر عملکرد مدل‌ها داشته باشد. هر تابع فعالیت ویژگی‌ها و کاربردهای خاص خود را دارد و با توجه به نوع مسئله و داده‌ها، باید بهترین گزینه را انتخاب کرد. با شناخت دقیق این توابع و نحوه عملکرد آنها، می‌توانید شبکه‌های عصبی قوی‌تر و دقیق‌تری طراحی کنید.

اگر میخواهید مفاهیم شبکه‌های عصبی و دیپ‌لرنینگ ر اصولی و مرحبه به مرحله بیاموزید، دوره جامع یادگیری عمیق زیر را به شما توصیه می‌کنم.

دوره جامع یادگیری عمیق: تسلط بر هوش مصنوعی با 40 ساعت آموزش (Tensorflow/keras)

همه چیز درباره توابع فعالیت (Activation Functions) در شبکه‌های عصبی و مشکل محو شدگی گرادیان

تعریف تابع فعالیت

چرا تابع فعالیت مهم است؟

چرا Sigmoid مشکل محو شدگی گرادیان دارد؟